GASTO VOLUMETRICO
El caudal volumétrico o tasa de flujo de fluidos es el volumen de fluido que pasa por una superficie dada en un tiempo determinado. Usualmente es representado con la letra Q mayúscula.
Algunos ejemplos de medidas de caudal volumétrico son: los metros cúbicos por segundo (m3/s, en unidades básicas del Sistema Internacional) y el pie cúbico por segundo (cu ft/s en el sistema inglés de medidas).
Dada un área A, sobre la cual fluye un fluido a una velocidad uniforme v con un ángulo  desde la dirección perpendicular a A, la tasa del caudal volumétrico es:
desde la dirección perpendicular a A, la tasa del caudal volumétrico es:
 desde la dirección perpendicular a A, la tasa del caudal volumétrico es:
desde la dirección perpendicular a A, la tasa del caudal volumétrico es:
En el caso de que el caudal sea perpendicular al área A, es decir,  , la tasa del flujo volumétrico es:1
, la tasa del flujo volumétrico es:1
 , la tasa del flujo volumétrico es:1
, la tasa del flujo volumétrico es:1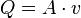
- Medición del flujo volumétrico
- Se acepta que el flujo volumétrico significa el volumen de un medio que se mueve a través de una sección transversal dentro de un período de tiempo dado.
- Q: flujo volumétrico en [m³/s], [l/min], [m³/h]
- V: volumen en [cm³], [dm³], [m³]
- t: tiempo en [s], [min], [h],
- Velocidad de flujo en un tubo
- La siguiente relación aplica adicionalmente a líquidos y gases:
- V: flujo volumétrico en [m³/s]
- c : velocidad de flujo media en [m/s]
- A : sección transversal en el punto pertinente en [m²]
- Donde se conoce la superficie de la sección transversal (tubos, canales) se puede usar esta fórmula para calcular el flujo volumétrico, siempre que se mida la velocidad del flujo.
- Como la velocidad de flujo a través de una sección transversal no es constante (véase la representación), la velocidad de flujo media c se determina por integración (véase cálculo integral):
- C: velocidad en un punto de la sección transversal (función del emplazamiento => f(xy) si la dirección del flujo es = z)
-
Qué es el flujo volumétrico.Strateger GraphicsEl flujo volumétrico es la determinación del flujo medido y expresado en unidades de , en comparación con el flujo de masa que se mide y se expresa en unidades de peso. Las mediciones de flujo volumétrico y las mediciones de flujo de masa se aplican tanto a los sistemas de flujo de líquido que fluye o sistemas de . Cada trae consigo consideraciones especiales con el fin de hacer la expresión de las unidades de flujo comprensibles y coherentes para todos los implicados. Esto se debe a que en muchos casos, la expresión de flujo volumétrico se refiere a una transacción o compra comercial y todas las partes deben estar hablando el mismo idioma.
Gas natural
Los consumidores que usan gas pagan sus cuentas sobre la base de miles de metros cúbicos. Dado que la masa o el peso, una función básica del número real de moléculas de gas natural o cualquier gas varía como una función de la presión de flujo y la temperatura, la expresión volumétrica de miles de pies cúbicos se expresa siempre en condiciones estándar, que por convención para la industria del gas en América del Norte es de Ps = 14,73 psia y Ts = 60 grados F (15 grados Celsius). Esto fija el número exacto de moléculas por metro cúbico para que pies (30,48 cm) cúbicos signifique lo mismo sin importar dónde se compra el gas, ya que una presión más alta con un fijo volumen significaría más moléculas y una temperatura más alta con el volumen fijo significaría menos moléculas.Otros gases
El flujo se expresa generalmente como el volumen estándar que fluye más allá de un área de sección transversal conocida a una velocidad media dada. Así que si la velocidad promedio del aire que pasa por una sección de 1 pie (30,48 cm) cuadrado de conducto es de 60 pies (18,29 m) por minuto, la velocidad de flujo volumétrico sería 60 pies (18,29 m) cúbicos en un minuto, o 1 pie (30,48 cm) cúbico por segundo.Los caudales volumétricos líquidos son algo más fáciles de entender, debido a la no compresibilidad básica de los líquidos en comparación con los gases, aunque la mayoría de las expresiones volumétricas de líquidos también se calculan en condiciones normales, debido a ligeras variaciones en la masa como los cambios de temperatura.Conversión de unidades
Las fórmulas de conversión estándar permiten que pies (30,48 cm) cúbicos por minuto sean convertidos en galones (3,79 l) por minuto, litros por minuto, por hora o por segundo. Las pequeñas unidades de pequeñas cantidades de gas utilizadas en laboratorios y hospitales serían centímetros cúbicos por minuto. Del mismo modo, los mililitros se aplican a las tasas de flujo de líquido métricas, mientras que litros por minuto se aplican a los flujos más grandes. Hay calculadoras en tiempo real a la derecha en la web que llevarán a cualquier gas o unidades de flujo de líquido y los convertirán a cualquier otro con sólo pulsar un botón.Convenciones diferentes
Muchos están confundidos con los flujos volumétricos y de masas. Las expresiones de flujo de masas tienden a ser utilizadas en aplicaciones científicas, aunque no siempre y las expresiones volumétricas prevalecen en aplicaciones comerciales como la compra de un cuarto de galón (1,14 l) de leche.Consideremos el movimiento de un objeto de volumen V y masa M que cae a través de un fluido con viscosidad cero (sin rozamiento).- Dibuja las fuerzas que actúan sobre el cuerpo.
- ¿La aceleración del objeto en caída es independiente de su masa?, ¿y de su volumen?
PROBLEMAS DE GASTO HIDRÁULICODisponemos de una plancha de corcho de 1 dm de espesor. Calcular la superficie mínima que se debe emplear para que flote en agua, sosteniendo a un naúfrago de 70 kg. La densidad del corcho es de 0.24 g/cm2.
Nota: entendemos por superficie mínima la que permite mantener al hombre completamente fuera del agua aunque la tabla esté totalmente inmersa en ella.Un cable anclado en el fondo de un lago sostiene una esfera hueca de plástico bajo su superficie.El volumen de la esfera es de 0.3 m3 y la tensión del cable 900 N. - ¿Qué masa tiene la esfera?
- El cable se rompe y la esfera sube a la superficie. Cuando está en equilibrio, ¿qué fracción del volumen de la esfera estará sumergida?.
Densidad del agua de mar 1.03 g/cm3Un depósito de agua está cerrado por encima con una placa deslizante de 12 m2 y 1200 kg de peso. El nivel del agua en el depósito es de 3.5 m de altura. Calcular la presión en el fondo. Si se abre un orificio circular de 5 cm de radio a medio metro por encima del fondo, calcúlese el volumen de agua que sale por segundo por este orificio. (Se considera que el área del orificio es muy pequeño frente al área del depósito).Dato: la presión atmosférica es de 105 PaLa prensa hidráulica de la figura está formada por dos depósitos cilíndricos, de diámetros 10 y 40 cm respectivamente, conectados por la parte inferior mediante un tubo, tal como se indica en la figura. Contienen dos líquidos inmiscibles: agua, de densidad 1 g/cm3 y aceite 0.68 g/cm3.Determinar el valor de la masa m para que el sistema esté en equilibrio.Tomar g=9.8 m/s2.Presión atmosférica = 101293 Pa.El depósito de la figura contiene agua. a) Si abrimos la llave de paso, ¿qué altura tendrá el agua en cada lado del depósito cuando se alcance el equilibrio?b) ¿qué cantidad de agua pasará de un recipiente al otro hasta que se alcance el equilibrio?De un gran depósito de agua, cuyo nivel se mantiene constante fluye agua que circula por los conductos de la figura hasta salir por la abertura D, que está abierta al aire. La diferencia de presión entre los puntos A y B es PB - PA = 500 Pa.Sabiendo que las secciones de los diferentes tramos de la conducción son SA= SC = 10 cm2 y SB=20 cm2, calcular las velocidades y las presiones del agua en los puntos A, B, C, de la conducción.La presión en C es la atmosférica, igual a 105 Pa.Para saber la velocidad del agua en una tubería empalmamos en ella un tubo en forma de T de menor sección, colocamos tubos manométricos A y B, como indica la figura y medimos la diferencia de altura (5 cm) entre los niveles superiores del líquido en tales tubos. - Sabiendo que la sección del tubo estrecho es 10 veces menor que la tubería, calcular la velocidad del líquido en ésta.
- Calcúlese el gasto, si el área de la sección mayor es 40 cm2
TEOREMA DE BERNOULLI Y SUS APLICACIONES"Un fluido no viscoso se mueve a 10 cm/seg por un tubo horizontal de 1 cm de radio, cuya presión interior es de 10 Pa. Luego el tubo se ramifica en varios tubos horizontales de 0,5 cm de radio cada uno. Sabiendo que la densidad del fluido es de 2 kg/lt y que la velocidad en cada tubo de la ramificación es de 8 cm/seg: a) Determinar en cuántos tubos se ramificó el tubo original. b) Calcular la presión en cada uno de los conductos luego de la ramificación."
Asumiremos que todos los caños, que son horizontales, se encuentran al mismo nivel. El esquema de los caños es, "visto desde arriba":
a) Como tenemos el radio del tubo de entrada, y de cada uno de los de salida, y las velocidades en los caños, podemos relacionar estos datos para plantear la igualdad entre el caudal entrante y el saliente:
Qentrante = Qsaliente
El caudal entrante es el caudal que pasa por el caño donde está el punto A:
Qentrante = vA . SA
El caudal saliente es la suma de todos los caudales en las ramificaciones 1, 2.... hasta X. Como todos los caños de la ramificación son iguales, y la velocidad en todos ellos es la misma (dato), entonces el caudal por cada caño de la ramificación será el mismo... por lo cual el caudal saliente total, va a ser el caudal que pasa por UNO de los caños de la ramificación, multiplicado por la cantidad de caños (que llamaremos X). Entonces:
Qsaliente = X . vB . SB
Igualando el caudal entrante con el saliente, queda:
vA . SA = X . vB . SB
10 cm/s . π . (1 cm)^2 = X . 8 cm/s . π . (0,5 cm)^2
Simplificando y despejando X, queda:
X = 5 . Así que, el tubo original se ramificó en 5 tubos. (Respuesta a))
b) Se pide la presión en uno de los tubos de la ramificación. Para eso, planteamos el teorema de Bernoullli entre A y B:
Como todo el sistema se encuentra a un mismo nivel, entonces HA = HB = 0. Las velocidades vA y vB se conocen, la densidad también, y pA también, siendo pB la incógnita. Reemplazamos todo:
10 Pa + (1/2) . 2000 kg/m^3 . (0,1 m/s)^2 = pB + (1/2) . 2000 kg/m^3 . (0,08 m/s/s)^2
10 Pa + 10 Pa = pB + 6,4 Pa
pB = 13,6 Pa Respuesta b)Notar que, si planteáramos Bernoulli entre el caño principal y otro de los tubos de la ramificación, obtendríamos la misma presión (13,6 Pa), ya que en todos los tubos de la ramificación la velocidad es la misma, y entonces la ecuación de Bernoulli quedaría con los mismos números.Ecuación de continuidad
En física, una ecuación de continuidad expresa una ley de conservación de forma matemática, ya sea de forma integral como de forma diferencial.Teoría electromagnética
En teoría electromagnética, la ecuación de continuidad viene derivada de dos de las ecuaciones de Maxwell. Establece que la divergencia de la densidad de corriente es igual al negativo de la derivada de ladensidad de carga respecto del tiempo:En otras palabras, sólo podrá haber un flujo de corriente si la cantidad de carga varía con el paso del tiempo, ya que esta disminuye o aumenta en proporción a la carga que es usada para alimentar dicha corriente.Esta ecuación establece la conservación de la carga.Mecánica de fluidos
En mecánica de fluidos, una ecuación de continuidad es una ecuación de conservación de la masa. Su forma diferencial es:donde es la densidad, t el tiempo y
es la densidad, t el tiempo y 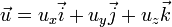 la velocidad del fluido. Es una de las tres ecuaciones de Euler.
la velocidad del fluido. Es una de las tres ecuaciones de Euler.Mecánica cuántica
En Mecánica cuántica, una ecuación de continuidad es una ecuación de conservación de la probabilidad. Su forma diferencial es:1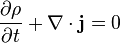 Donde
Donde es la densidad de probabilidad de la función de ondas y
es la densidad de probabilidad de la función de ondas y 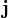 es la corriente de probabilidad o densidad de corriente. Estas dos expresiones se pueden relacionar con la función de onda de una partícula como:
es la corriente de probabilidad o densidad de corriente. Estas dos expresiones se pueden relacionar con la función de onda de una partícula como:
Mecánica relativista
En la teoría especial de la relatividad, una ecuación de continuidad debe escribirse en forma covariante, por lo que la ecuación de continuidad usual para la carga eléctrica y otras magnitudes conservadas se suele escribir en teoría de la relatividad como: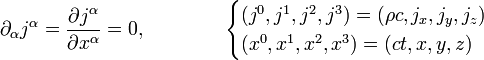 La ecuación de continuidad para la densidad másica (o más exactamente la energía másica) y la densidad de momento lineal se escribe en términos del tensor energía impulso:
La ecuación de continuidad para la densidad másica (o más exactamente la energía másica) y la densidad de momento lineal se escribe en términos del tensor energía impulso: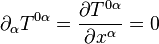 En el contexto de la teoría general de la relatividad las derivadas parciales deben substituirse por derivadas covariantes:
En el contexto de la teoría general de la relatividad las derivadas parciales deben substituirse por derivadas covariantes: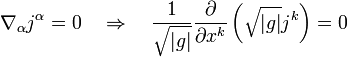 Donde
Donde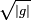 es la raíz del determinante del tensor métrico asociado a las coordenadas
es la raíz del determinante del tensor métrico asociado a las coordenadas  . Y análogamente para la conservación de la energía:
. Y análogamente para la conservación de la energía: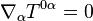



 =
=  =
=  =
=  =
=  = altura en la dirección de la
= altura en la dirección de la  (donde
(donde  ) para dar lugar a la llamada altura piezo métrica o también carga piezométrica.[
) para dar lugar a la llamada altura piezo métrica o también carga piezométrica.[
 , de esta forma el término relativo a la velocidad se llamará presión dinámica, los términos de presión y altura se agrupan en la presión estática.
, de esta forma el término relativo a la velocidad se llamará presión dinámica, los términos de presión y altura se agrupan en la presión estática.




 es una constante-
es una constante-



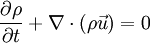
grasias es muy explisito
ReplyDelete