Dilatación
Se denomina dilatación térmica al aumento de longitud, volumen o alguna otra dimensión métrica que sufre un cuerpo físico debido al aumento de temperatura que se provoca en él por cualquier medio. La contracción térmica es la disminución de propiedades métricas por disminución de la misma.
Dilatación lineal[editar]
Es aquella en la cual predomina la variación en una única dimensión, o sea, en el ancho, largo o altura del cuerpo. El coeficiente de dilatación lineal, designado por αL, para una dimensión lineal cualquiera, se puede medir experimentalmente comparando el valor de dicha magnitud antes y después:
Donde  , es el incremento de su integridad física cuando se aplica un pequeño cambio global y uniforme de temperatura
, es el incremento de su integridad física cuando se aplica un pequeño cambio global y uniforme de temperatura 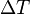 a todo el cuerpo. El cambio total de longitud de la dimensión lineal que se considere, puede despejarse de la ecuación anterior:
a todo el cuerpo. El cambio total de longitud de la dimensión lineal que se considere, puede despejarse de la ecuación anterior:
 , es el incremento de su integridad física cuando se aplica un pequeño cambio global y uniforme de temperatura
, es el incremento de su integridad física cuando se aplica un pequeño cambio global y uniforme de temperatura 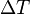 a todo el cuerpo. El cambio total de longitud de la dimensión lineal que se considere, puede despejarse de la ecuación anterior:
a todo el cuerpo. El cambio total de longitud de la dimensión lineal que se considere, puede despejarse de la ecuación anterior:
Donde:
- α=coeficiente de dilatación lineal [°C-1]
- L0 = Longitud inicial
- Lf = Longitud final
- T0 = Temperatura inicial.
- Tf = Temperatura final
Dilatación volumétrica[editar]
Es el coeficiente de dilatación volumétrico, designado por αV, se mide experimentalmente comparando el valor del volumen total de un cuerpo antes y después de cierto cambio de temperatura como, y se encuentra que en primera aproximación viene dado por:
Experimentalmente se encuentra que un sólido isótropo tiene un coeficiente de dilatación volumétrico que es aproximadamente tres veces el coeficiente de dilatación lineal. Esto puede probarse a partir de la teoría de la elasticidad lineal. Por ejemplo si se considera un pequeño prisma rectangular (de dimensiones: Lx, Ly y Lz), y se somete a un incremento uniforme de temperatura, el cambio de volumen vendrá dado por el cambio de dimensiones lineales en cada dirección:
Esta última relación prueba que 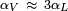 , es decir, el coeficiente de dilatación volumétrico es numéricamente unas 3 veces el coeficiente de dilatación lineal de una barra del mismo material.
, es decir, el coeficiente de dilatación volumétrico es numéricamente unas 3 veces el coeficiente de dilatación lineal de una barra del mismo material.
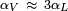 , es decir, el coeficiente de dilatación volumétrico es numéricamente unas 3 veces el coeficiente de dilatación lineal de una barra del mismo material.
, es decir, el coeficiente de dilatación volumétrico es numéricamente unas 3 veces el coeficiente de dilatación lineal de una barra del mismo material.Dilatación de área[editar]
Cuando un área o superficie se dilata, lo hace incrementando sus dimensiones en la misma proporción. Por ejemplo, una lámina metálica aumenta su largo y ancho, lo que significa un incremento de área. La dilatación de área se diferencia de la dilatación lineal porque implica un incremento de área.
El coeficiente de dilatación de área es el incremento de área que experimenta un cuerpo de determinada sustancia, de área igual a la unidad, al elevarse su temperatura un grado centígrado. Este coeficiente se representa con la letra griega gamma (γ). El coeficiente de dilatación de área se usa para los sólidos. Si se conoce el coeficiente de dilatación lineal de un sólido, su coeficiente de dilatación de área será dos veces mayor:
Al conocer el coeficiente de dilatación de área de un cuerpo sólido se puede calcular el área final que tendrá al variar su temperatura con la siguiente expresión:
Donde:
- γ=coeficiente de dilatación de área [°C-1]
- A0 = Área inicial
- Af = Área final
- T0 = Temperatura inicial.
- Tf = Temperatura final
Causa de la dilatación[editar]
En un sólido las moléculas tienen una posición razonablemente fija dentro de él. Cada átomo de la red cristalina vibra sometido a una fuerza asociada a un pozo de potencial, la amplitud del movimiento dentro de dicho pozo dependerá de la energía total de átomo o molécula. Al absorber calor, la energía cinética promedio de las moléculas aumenta y con ella la amplitud media del movimiento vibracional (ya que la energía total será mayor tras la absorción de calor). El efecto combinado de este incremento es lo que da el aumento de volumen del cuerpo.
En los gases el fenómeno es diferente, ya que la absorción de calor aumenta la energía cinética media de las moléculas lo cual hace que la presión sobre las paredes del recipiente aumente. El volumen final por tanto dependerá en mucha mayor medida del comportamiento de las paredes.


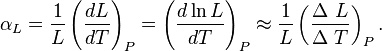
![L_f = L_0 [1 +\alpha_L (T_f - T_0)]\;](https://upload.wikimedia.org/math/4/d/8/4d8d9e521d59aa36de0d776706db3b16.png)

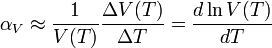


![A_f = A_0 [1 +\gamma_A (T_f - T_0)]\;](https://upload.wikimedia.org/math/8/4/4/84444b9c6e865aaf0b6d1376be7a9a6b.png)