Teorema de Torricelli
El teorema de Torricelli o principio de Torricelli es una aplicación del principio de Bernoulli y estudia el flujo de un líquido contenido en un recipiente, a través de un pequeño orificio, bajo la acción de la gravedad.
La velocidad de un líquido en una vasija abierta, por un orificio, es la que tendría un cuerpo cualquiera, cayendo libremente en el vacío desde el nivel del líquido hasta el centro de gravedad del orificio.
Matemáticamente:
donde:
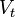 es la velocidad teórica del líquido a la salida del orificio
es la velocidad teórica del líquido a la salida del orificio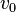 es la velocidad de aproximación o inicial.
es la velocidad de aproximación o inicial.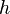 es la distancia desde la superficie del líquido al centro del orificio.
es la distancia desde la superficie del líquido al centro del orificio.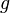 es la aceleración de la gravedad
es la aceleración de la gravedad
Para velocidades de aproximación bajas, la mayoría de los casos, la expresión anterior se transforma en:
donde:
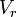 es la velocidad real media del líquido a la salida del orificio
es la velocidad real media del líquido a la salida del orificio es el coeficiente de velocidad. Para cálculos preliminares en aberturas de pared delgada puede admitirse 0,95 en el caso más desfavorable.
es el coeficiente de velocidad. Para cálculos preliminares en aberturas de pared delgada puede admitirse 0,95 en el caso más desfavorable.
tomando  =1
=1
 =1
=1
Experimentalmente se ha comprobado que la velocidad media de un chorro de un orificio de pared delgada, es un poco menor que la ideal, debido a la viscosidad del fluido y otros factores tales como la tensión superficial, de ahí el significado de este coeficiente de velocidad.
Caudal descargado[editar]
El caudal o volumen del fluido que pasa por el orificio en un tiempo, 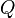 , puede calcularse como el producto de
, puede calcularse como el producto de  , el área real de la sección contraída, por
, el área real de la sección contraída, por 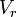 , la velocidad real media del fluido que pasa por esa sección, y por consiguiente se puede escribir la siguiente ecuación:
, la velocidad real media del fluido que pasa por esa sección, y por consiguiente se puede escribir la siguiente ecuación:
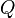 , puede calcularse como el producto de
, puede calcularse como el producto de  , el área real de la sección contraída, por
, el área real de la sección contraída, por 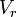 , la velocidad real media del fluido que pasa por esa sección, y por consiguiente se puede escribir la siguiente ecuación:
, la velocidad real media del fluido que pasa por esa sección, y por consiguiente se puede escribir la siguiente ecuación:
en donde
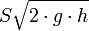 representa la descarga ideal que habría ocurrido si no estuvieran presentes la fricción y la contracción.
representa la descarga ideal que habría ocurrido si no estuvieran presentes la fricción y la contracción.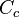 es el coeficiente de contracción de la vena fluida a la salida del orificio. Su significado radica en el cambio brusco de sentido que deben realizar las partículas de la pared interior próximas al orificio. Es la relación entre el área contraída
es el coeficiente de contracción de la vena fluida a la salida del orificio. Su significado radica en el cambio brusco de sentido que deben realizar las partículas de la pared interior próximas al orificio. Es la relación entre el área contraída  y la del orificio
y la del orificio 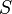 . Suele estar en torno a 0,65.
. Suele estar en torno a 0,65.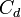 es el coeficiente por el cual el valor ideal de descarga es multiplicado para obtener el valor real, y se conoce como coeficiente de descarga. Numéricamente es igual al producto de los otros dos coeficientes.
es el coeficiente por el cual el valor ideal de descarga es multiplicado para obtener el valor real, y se conoce como coeficiente de descarga. Numéricamente es igual al producto de los otros dos coeficientes. 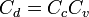
El coeficiente de descarga variará con la carga y el diámetro del orificio. Sus valores para el agua han sido determinados y tabulados por numerosos experimentadores. De forma orientativa se pueden tomar valores sobre 0,6. Así se puede apreciar la importancia del uso de estos coeficientes para obtener unos resultados de caudal aceptables
.

Aplicación Teorema de Torricelli 0001
Un recipiente cilíndrico se llena de un líquido hasta alcanzar un metro de altura con respecto a la base del recipiente. A continuación se hace un orificio en un punto situado 20 cm por debajo del nivel del recipiente:
a) ¿Cuál es la velocidad de salida del líquido a través del orificio?
b) ¿A qué distancia del recipiente caerá la primera gota de líquido que toque el suelo?
a) ¿Cuál es la velocidad de salida del líquido a través del orificio?
b) ¿A qué distancia del recipiente caerá la primera gota de líquido que toque el suelo?
SOLUCIÓN
a) La velocidad de salida del líquido a través del orificio viene dada por la expresión: 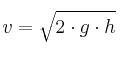
Según nos dice el enunciado, el agujero se hace a una altura de 0,8 m con respecto a la base del recipiente:
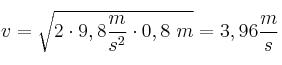
b) Para calcular la distancia a la que cae la primera gota debemos considerar que ésta sigue un movimiento semejante a un lanzamiento horizontal. En ese caso, la posición con respeto al eje X sigue la ecuación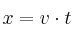 , mientras que la posición en el eje Y sigue la ecuación
, mientras que la posición en el eje Y sigue la ecuación 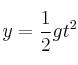 . Como sabemos que la gota comienza a una altura de 0,8 m:
. Como sabemos que la gota comienza a una altura de 0,8 m:
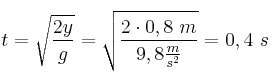
Para saber la posición horizontal sustituimos este tiempo:
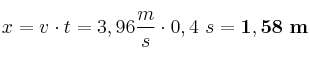
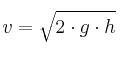
Según nos dice el enunciado, el agujero se hace a una altura de 0,8 m con respecto a la base del recipiente:
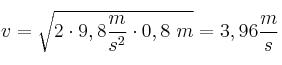
b) Para calcular la distancia a la que cae la primera gota debemos considerar que ésta sigue un movimiento semejante a un lanzamiento horizontal. En ese caso, la posición con respeto al eje X sigue la ecuación
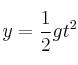 . Como sabemos que la gota comienza a una altura de 0,8 m:
. Como sabemos que la gota comienza a una altura de 0,8 m: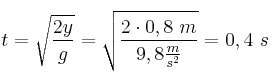
Para saber la posición horizontal sustituimos este tiempo:
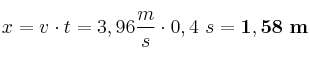
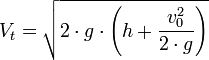


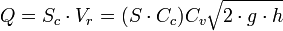
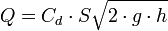
No comments:
Post a Comment